本文主要讲解关于路径规划 | 详解混合A*算法Hybrid A*(附ROS C++/Python/Matlab仿真)相关内容,让我们来一起学习下吧!
目录
- 0 专栏介绍
- 1 为什么需要Hybrid A*算法?
- 2 Hybrid A*算法原理
-
- 2.1 基本流程
- 2.2 运动学约束启发式
- 2.3 基于维诺图的路径耗散
- 2.4 连续性节点扩展
- 3 算法仿真
-
- 3.1 ROS C++ 仿真
- 3.2 Python仿真
- 3.3 Matlab仿真
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 为什么需要Hybrid A*算法?
混合A*算法(Hybrid A*)是一种改进的路径规划算法,用于解决普通A*算法在某些情况下的局限性。接下来简单介绍A*算法的不足,更详细的A*算法原理请看路径规划 | 图解A*、Dijkstra、GBFS算法的异同(附C++/Python/Matlab仿真)
- 高维连续空间的问题: A*算法在高维连续空间中效率较低,因为它需要将连续空间离散化为网格,这会导致维度爆炸,计算量增加;
- 运动约束的问题: 在车辆或机器人路径规划中,通常需要考虑车辆或机器人的运动约束,例如转弯半径、最大速度等。普通的A*算法不考虑这些运动约束,因此可能会生成无法执行的路径。
混合A*算法成功应用于由美国政府在2007年组织的DARPA城市挑战机器人比赛中。随后,Dolgov等人在中对该算法进行了进一步研究。混合A*算法的行为类似于A*算法,关键区别在于状态转换发生在连续而非离散空间中。虽然混合A*搜索隐含地在离散化的网格上构建图形,但顶点可以达到网格中的任何连续点。为了处理连续搜索空间的无限性,采用了网格单元格的离散化形式,从而限制了图形的增长。通常,搜索空间是三维的,连续状态空间包括
x
x
x,
y
y
y和
θ
theta
θ——而A*算法只有离散的
x
x
x和
y
y
y状态
2 Hybrid A*算法原理
2.1 基本流程
Hybrid A*算法流程如表所示,主要分为启发式搜索和轨迹优化两个阶段。
本文聚焦于第一阶段启发式搜索,也即路径规划部分。Hybrid A*采用的共轭梯度轨迹优化技术将在后续教程单独分析。对比一下Hybrid A*的规划算法和路径规划 | 图解A*、Dijkstra、GBFS算法的异同(附C++/Python/Matlab仿真)中的A*算法流程,可以发现几乎是一模一样的,下面重点分析几个不同的地方。
2.2 运动学约束启发式
A*算法的启发式函数一般采用当前点到目标点的欧氏距离,Hybrid A*算法则向启发式函数进一步引入运动学约束
h
(
n
)
=
max
{
C
o
n
s
t
r
a
i
n
e
d
C
o
s
t
,
U
n
c
o
n
s
t
r
a
i
n
e
d
C
o
s
t
}
hleft( n right) =max left{ mathrm{ConstrainedCost},mathrm{UnconstrainedCost} right}
h(n)=max{ConstrainedCost,UnconstrainedCost}
其中:
-
C
o
n
s
t
r
a
i
n
e
d
C
o
s
t
mathrm{ConstrainedCost}
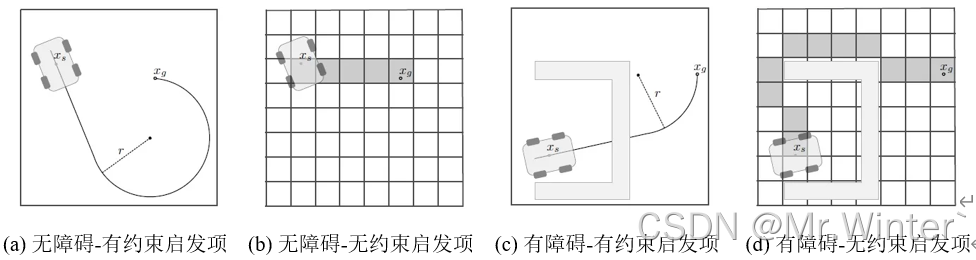
ConstrainedCost:只考虑车辆的非完整运动学约束而不考虑障碍物的有约束启发项(Constrained heuristics),通常采用Dubins或Reeds-Shepp曲线计算该项损失。
- Dubins曲线是指由美国数学家 Lester Dubins 在20世纪50年代提出的一种特殊类型的最短路径曲线。这种曲线通常用于描述在给定转弯半径下的无人机、汽车或船只等载具的最短路径,其特点是起始点和终点处的切线方向和曲率都是已知的,Dubins曲线包括直线段和最大转弯半径下的圆弧组成,通过合适的组合可以实现从一个姿态到另一个姿态的最短路径规划。更详细的算法原理请看曲线生成 | 图解Dubins曲线生成原理(附ROS C++/Python/Matlab仿真);
- Reeds-Shepp曲线是一种用于描述在平面上从一个点到另一个点最优路径的数学模型。这种曲线是由美国数学家 J. A. Reeds 和 L. A. Shepp 在1990年提出的,它被广泛应用于路径规划和运动规划问题中,具有最优性、约束性和多样性,更详细的算法原理请看曲线生成 | 图解Reeds-Shepp曲线生成原理(附ROS C++/Python/Matlab仿真);
- 只考虑障碍物信息而不考虑车辆运动学特性的无约束启发项(Unconstrained heuristics),通常采用Dijkstra或A*算法计算该项损失。
如图所示,可视化了不同类型的启发项。当环境障碍不影响规划路径时,有约束启发项损失往往大于无约束,因为后者没有考虑朝向和运动限制;当环境障碍影响规划路径时,有约束启发项损失往往小于无约束,因为后者会进行避障。因此对两项取
max
max
max算子可以综合障碍影响和运动学特性,更符合真实情况。
2.3 基于维诺图的路径耗散
路径耗散函数可选为
g
(
n
)
=
∑
i
d
x
i
⋅
t
u
r
n
i
⋅
r
e
v
e
r
i
⋅
s
w
i
t
c
h
i
gleft( n right) =sum_i^{}{mathrm{d}x_icdot mathrm{turn}_icdot mathrm{rever}_icdot mathrm{switch}_i}
g(n)=i∑dxi⋅turni⋅reveri⋅switchi
其中
d
x
i
mathrm{d}x_i
dxi是第
i
i
i步的运动长度;
t
u
r
n
i
mathrm{turn}_i
turni是第
i
i
i步的转弯惩罚(趋于选择直行);
r
e
v
e
r
i
mathrm{rever}_i
reveri是第
i
i
i步的反向惩罚;
s
w
i
t
c
h
i
mathrm{switch}_i
switchi是第
i
i
i步的变向惩罚。
路径耗散也用Voronoi势场函数度量
g
(
n
)
=
∑
n
ρ
V
(
n
x
,
n
y
)
gleft( n right) =sumnolimits_n^{}{rho _Vleft( n_x,n_y right)}
g(n)=∑nρV(nx,ny),其中
ρ
V
(
x
,
y
)
=
(
α
α
+
d
O
(
x
,
y
)
)
(
d
V
(
x
,
y
)
d
O
(
x
,
y
)
+
d
V
(
x
,
y
)
)
(
d
O
−
d
O
max
)
2
(
d
O
max
)
2
;
d
O
<
d
O
max
rho _Vleft( x,y right) =left( frac{alpha}{alpha +d_{mathcal{O}}left( x,y right)} right) left( frac{d_{mathcal{V}}left( x,y right)}{d_{mathcal{O}}left( x,y right) +d_{mathcal{V}}left( x,y right)} right) frac{left( d_{mathcal{O}}-d_{mathcal{O}}^{max} right) ^2}{left( d_{mathcal{O}}^{max} right) ^2};d_{mathcal{O}}<d_{mathcal{O}}^{max}
ρV(x,y)=(α+dO(x,y)α)(dO(x,y)+dV(x,y)dV(x,y))(dOmax)2(dO−dOmax)2;dO<dOmax
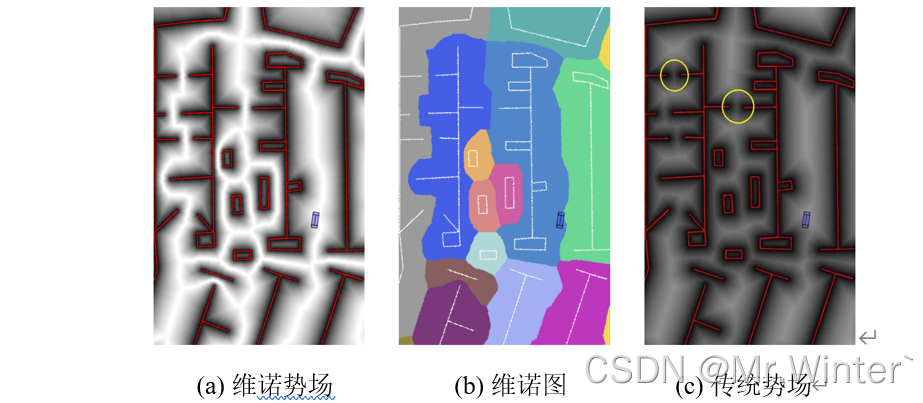
如图所示,Voronoi势场函数通过引入维诺图,使机器人可以很好地通过狭窄路段,而这些路段在传统势场方法中会产生高势垒,阻碍机器人运动
更详细的关于维诺图的构建算法原理,请看
- 地图结构 | 图解维诺图Voronoi原理(附C++/Python/Matlab仿真)
- 路径规划 | 详解维诺图Voronoi算法(附ROS C++/Python/Matlab仿真)
2.4 连续性节点扩展
搜索从车辆的当前状态
x
s
x_s
xs开始。Hybrid A*将生成六个后继顶点,其中三个向前驾驶,另外三个向后驾驶,如图所示
后继顶点通过使用车辆的最小转弯半径的弧线生成,以确保生成的路径在实际中是可行的。如下面代码所示描述了上图的状态转换方式
double R = 1.3;
// // 20 deg 0.349065 rad
double alpha = 14 * M_PI / 180;
// R, alpha
double dy[] = { 0, -R * (1 - cos(alpha)), R * (1 - cos(alpha)) };
double dx[] = { alpha * R, R * sin(alpha), R * sin(alpha) };
double dt[] = { 0, alpha, -alpha };
状态转换的成本基于弧线的长度。额外的成本会因为改变驾驶方向、倒车以及转弯而产生,而不是直行。转弯和倒车的惩罚是乘法的(取决于路径转弯或倒车的比例),而改变驾驶方向的惩罚是恒定的。
3 算法仿真
3.1 ROS C++ 仿真
核心代码如下所示
// main process
while (!open_list.empty())
{
// pop current node from open list
HybridNode current = open_list.top();
open_list.pop();
// current node does not exist in closed list
if (closed_list.find(current.id_) != closed_list.end())
continue;
closed_list.insert(std::make_pair(current.id_, current));
expand.emplace_back(current.x_, current.y_, 0, 0, _worldToIndex(current.x_, current.y_));
// goal shot
std::vector<Node> path_dubins;
if (std::hypot(current.x_ - goal.x_, current.y_ - goal.y_) < 50)
{
if (dubinsShot(current, goal, path_dubins))
{
path = _convertClosedListToPath(closed_list, start, current);
std::reverse(path.begin(), path.end());
path.insert(path.end(), path_dubins.begin(), path_dubins.end());
std::reverse(path.begin(), path.end());
return true;
}
}
// explore neighbor of current node
for (size_t i = 0; i < dir; i++)
{
// explore a new node
HybridNode node_new = current + motions[i];
updateIndex(node_new);
// node_new in closed list
if (closed_list.find(node_new.id_) != closed_list.end())
continue;
// next node hit the boundary or obstacle
// prevent planning failed when the current within inflation
if ((_worldToIndex(node_new.x_, node_new.y_) < 0) || (_worldToIndex(node_new.x_, node_new.y_) >= ns_) ||
(node_new.t_ / DELTA_HEADING >= HEADINGS) ||
(global_costmap[_worldToIndex(node_new.x_, node_new.y_)] >= lethal_cost_ * factor_ &&
global_costmap[_worldToIndex(node_new.x_, node_new.y_)] >=
global_costmap[_worldToIndex(current.x_, current.y_)]))
continue;
node_new.pid_ = current.id_;
updateHeuristic(node_new);
open_list.push(node_new);
}
}
效果如下所示
3.2 Python仿真
核心代码如下所示:
# Run loop while path is found or open set is empty
while True:
counter +=1
# Check if openSet is empty, if empty no solution available
if not openSet:
return None
# Get first node in the priority queue
currentNodeIndex = costQueue.popitem()[0]
currentNode = openSet[currentNodeIndex]
# Revove currentNode from openSet and add it to closedSet
openSet.pop(currentNodeIndex)
closedSet[currentNodeIndex] = currentNode
# Get Reed-Shepp Node if available
rSNode = reedsSheppNode(currentNode, goalNode, mapParameters)
# Id Reeds-Shepp Path is found exit
if rSNode:
closedSet[index(rSNode)] = rSNode
break
# USED ONLY WHEN WE DONT USE REEDS-SHEPP EXPANSION OR WHEN START = GOAL
if currentNodeIndex == index(goalNode):
print("Path Found")
print(currentNode.traj[-1])
break
# Get all simulated Nodes from current node
for i in range(len(motionCommand)):
simulatedNode = kinematicSimulationNode(currentNode, motionCommand[i], mapParameters)
# Check if path is within map bounds and is collision free
if not simulatedNode:
continue
# Draw Simulated Node
x,y,z =zip(*simulatedNode.traj)
plt.plot(x, y, linewidth=0.3, color='g')
# Check if simulated node is already in closed set
simulatedNodeIndex = index(simulatedNode)
if simulatedNodeIndex not in closedSet:
# Check if simulated node is already in open set, if not add it open set as well as in priority queue
if simulatedNodeIndex not in openSet:
openSet[simulatedNodeIndex] = simulatedNode
costQueue[simulatedNodeIndex] = max(simulatedNode.cost , Cost.hybridCost * holonomicHeuristics[simulatedNode.gridIndex[0]][simulatedNode.gridIndex[1]])
else:
if simulatedNode.cost < openSet[simulatedNodeIndex].cost:
openSet[simulatedNodeIndex] = simulatedNode
costQueue[simulatedNodeIndex] = max(simulatedNode.cost , Cost.hybridCost * holonomicHeuristics[simulatedNode.gridIndex[0]][simulatedNode.gridIndex[1]])
3.3 Matlab仿真
核心代码如下所示:
while ~isempty(Open)
% pop the least cost node from open to close
[wknode,Open] = PopNode(Open,cfg);
[isok,idx] = inNodes(wknode,Close);
if isok
Close(idx) = wknode;
else
Close = [Close, wknode];
end
[isok,path] = AnalysticExpantion([wknode.x,wknode.y,wknode.theta],End,veh,cfg);
if isok
Close(end+1) = wknode;
Close(idx) = [];
[x,y,th,D,delta] = getFinalPath(path,Close,veh,cfg);
break
end
[Open,Close] = Update(wknode,Open,Close,veh,cfg); % 使用
end
完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇
以上就是关于路径规划 | 详解混合A*算法Hybrid A*(附ROS C++/Python/Matlab仿真)相关的全部内容,希望对你有帮助。欢迎持续关注程序员导航网,学习愉快哦!
转载请注明:路径规划 | 详解混合A*算法Hybrid A*(附ROS C++/Python/Matlab仿真) | 程序员导航网