本文主要讲解关于2024五一杯:煤矿深部开采冲击地压危险预测 (详细完整思路,已修改)相关内容,让我们来一起学习下吧!
背景
了解即可
煤炭是中国的主要能源和重要的工业原料。然而,随着开采深度的增加,地应力增大,井下煤岩动力灾害风险越来越大,严重影响着煤矿的安全高效开采。在各类深部煤岩动力灾害事故中,冲击地压已成为威胁中国煤矿安全生产最重要的灾害之一,冲击地压事故易造成严重的人员伤亡和财产损失。近年来,研究人员进行了大量深入的研究,采取了许多防控措施,中国煤矿安全形势持续稳步改善。但是,冲击地压事故仍时有发生,煤矿安全形势依然严峻,冲击地压的监测预警和有效防控仍是煤矿安全生产中亟待解决的科技问题。
重要背景
在深部煤矿开采过程中,可以监测声发射(AE)和电磁辐射(EMR)信号,电磁辐射和声发射传感器每30秒采集一个数据,可通过这些数据的变化趋势判断目前工作面或巷道是否存在冲击地压危险。
数据介绍:分类
电磁辐射和声发射数据随着采煤工作面的推进波动,一般在冲击地压发生前数天(如0-7天,即大约冲击地压发生前7天内)会有一些趋势性前兆特征,因此我们将电磁辐射和声发射数据分为5类,(A)正常工作数据;(B)前兆特征数据;©干扰信号数据;(D)传感器断线数据;(E)工作面休息数据,其中,A、B、C 类为工作面正常生产时的数据,D类为监测系统不正常时的数据,E类为停产期间的数据。
附件1给出了2019年1月9日-2020年1月7日采集的电磁辐射和声发射数据,并且标记出了所对应的A、B、C类以及D或者E类(D/E)数据。请建立数学模型,完成以下问题:
问题一
问题1:如图1,已知现场工作面的部分电磁辐射和声发射信号中存在大量干扰信号,有可能是工作面的其他作业或设备干扰等因素引起,这对后期的电磁辐射和声发射信号处理造成了一定的影响。应用附件1和2中的数据,完成以下问题。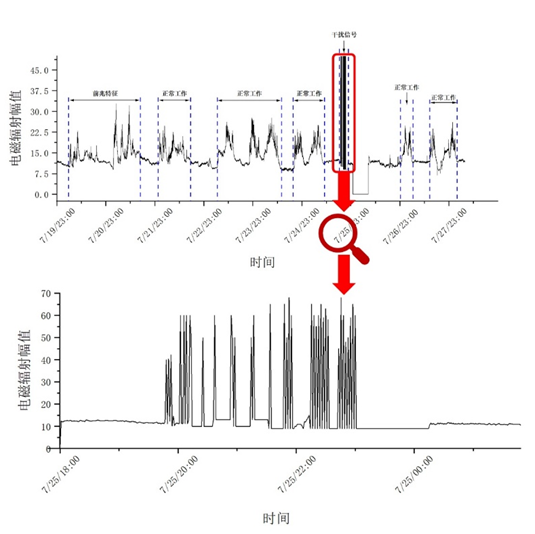
第一小问
建立数学模型,对存在干扰的电磁辐射和声发射信号进行分析,分别给出电磁辐射和声发射中的干扰信号数据的特征(不少于3个)。
第一问相当于是做特征工程,先提取干扰的数据进行分析,即类别C。做好只会,才能做下一问的模型预测识别。
第二小问
使用第一问选好的特征,开始建模(机器学习模型,或者时间序列模型,看哪个效果好吧),训练识别出对应实践的数据,填写到表中即可。
利用第一小问中得到的特征,建立数学模型,对2022年5月1日-2022年5月30日的电磁辐射和2022年4月1日-2022年5月30日及2022年10月10日-2022年11月10日声发射信号中的干扰信号所在的时间区间进行识别,分别给出电磁辐射和声发射最早发生的5个干扰信号所在的区间,完成表1和表2。
| 表1 电磁辐射干扰信号时间区间 | ||
|---|---|---|
| 序号 | 时间区间起点 | 时间区间终点 |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
| 表2 声发射干扰信号时间区间 | ||
|---|---|---|
| 序号 | 时间区间起点 | 时间区间终点 |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
具体思路
1. 数据预处理: 从附件1中提取所有干扰信号(分类为’C’的数据行)。 清理数据,确保时间和信号值格式正确,并处理可能存在的缺失值或异常值。
2计算统计干扰信号的特征(作为特征)
依次去前后一段时间内的数据计算一些特征,公式这里给一些可以做参考:(选择一部分计算即可)
-
平均值类
-
算术平均值:
T
F
1
=
1
N
∑
i
=
1
N
x
i
T_{F1} = frac{1}{N}sum_{i=1}^{N}x_i
TF1=N1∑i=1Nxi
-
绝对值平均值:
T
F
2
=
1
N
∑
i
=
1
N
∣
x
i
∣
T_{F2} = frac{1}{N}sum_{i=1}^{N}|x_i|
TF2=N1∑i=1N∣xi∣
-
算术平均值:
-
极值类
-
最小值:
T
F
3
=
min
(
x
1
,
x
2
,
.
.
.
,
x
N
)
T_{F3} = min(x_1, x_2, ..., x_N)
TF3=min(x1,x2,...,xN)
-
最大值:
T
F
4
=
max
(
x
1
,
x
2
,
.
.
.
,
x
N
)
T_{F4} = max(x_1, x_2, ..., x_N)
TF4=max(x1,x2,...,xN)
-
最小值:
-
标准差与方差类
-
标准差:
T
F
5
=
1
N
∑
i
=
1
N
(
x
i
−
x
ˉ
)
2
T_{F5} = sqrt{frac{1}{N} sum_{i=1}^{N}(x_i - bar{x})^2}
TF5=N1∑i=1N(xi−xˉ)2
-
方差:
T
F
6
=
1
N
∑
i
=
1
N
(
x
i
−
x
ˉ
)
2
T_{F6} = frac{1}{N} sum_{i=1}^{N}(x_i - bar{x})^2
TF6=N1∑i=1N(xi−xˉ)2
-
标准差:
-
波形因子与峰值因子
-
波形因子:
T
F
7
=
T
F
5
T
F
2
T_{F7} = frac{T_{F5}}{T_{F2}}
TF7=TF2TF5
-
峰值因子:
T
F
8
=
max
∣
x
i
∣
T
F
2
T_{F8} = frac{max|x_i|}{T_{F2}}
TF8=TF2max∣xi∣
-
波形因子:
-
频率中心
-
T
F
1
=
∑
f
(
x
k
)
⋅
X
(
k
)
∑
X
(
k
)
T_{F1} = frac{sum f(x_k) cdot X(k)}{sum X(k)}
TF1=∑X(k)∑f(xk)⋅X(k)
-
-
频率重心
-
T
F
2
=
∑
f
2
(
x
k
)
⋅
X
(
k
)
∑
X
(
k
)
T_{F2} = frac{sum f^2(x_k) cdot X(k)}{sum X(k)}
TF2=∑X(k)∑f2(xk)⋅X(k)
-
-
频率标准差
-
T
F
3
=
∑
(
f
(
x
k
)
−
f
0
)
2
⋅
X
(
k
)
∑
X
(
k
)
T_{F3} = sqrt{frac{sum (f(x_k) - f_0)^2 cdot X(k)}{sum X(k)}}
TF3=∑X(k)∑(f(xk)−f0)2⋅X(k)
-
-
频率变异系数
-
T
F
4
=
T
F
3
T
F
1
T_{F4} = frac{T_{F3}}{T_{F1}}
TF4=TF1TF3
-
-
平均频率
-
T
F
5
=
∑
f
(
x
k
)
⋅
X
(
k
)
K
T_{F5} = frac{sum f(x_k) cdot X(k)}{K}
TF5=K∑f(xk)⋅X(k)
-
-
均方根频率
-
T
F
6
=
∑
f
2
(
x
k
)
⋅
X
(
k
)
K
T_{F6} = sqrt{frac{sum f^2(x_k) cdot X(k)}{K}}
TF6=K∑f2(xk)⋅X(k)
-
-
标准化频率
-
T
F
7
=
∑
(
f
(
x
k
)
−
f
0
)
2
⋅
X
(
k
)
K
T_{F7} = frac{sum (f(x_k) - f_0)^2 cdot X(k)}{K}
TF7=K∑(f(xk)−f0)2⋅X(k)
-
-
波形因子
-
T
F
8
=
∑
(
X
(
k
)
)
2
∑
∣
X
(
k
)
∣
T_{F8} = frac{sqrt{sum (X(k))^2}}{sum |X(k)|}
TF8=∑∣X(k)∣∑(X(k))2
-
-
峰值因子
-
T
F
9
=
max
∣
X
(
k
)
∣
∑
∣
X
(
k
)
∣
T_{F9} = frac{max |X(k)|}{sum |X(k)|}
TF9=∑∣X(k)∣max∣X(k)∣
-
-
脉冲因子
-
T
F
10
=
max
∣
X
(
k
)
∣
∑
(
X
(
k
)
)
2
T_{F10} = frac{max |X(k)|}{sqrt{sum (X(k))^2}}
TF10=∑(X(k))2
max∣X(k)∣
-
-
裕度因子
-
T
F
11
=
max
∣
X
(
k
)
∣
(
∑
∣
X
(
k
)
∣
2
)
1
2
T_{F11} = frac{max |X(k)|}{(sum |X(k)|^2)^{frac{1}{2}}}
TF11=(∑∣X(k)∣2)21max∣X(k)∣
-
-
波峰因子
-
T
F
12
=
∑
(
f
(
x
k
)
−
f
0
)
3
⋅
X
(
k
)
K
T_{F12} = frac{sum (f(x_k) - f_0)^3 cdot X(k)}{K}
TF12=K∑(f(xk)−f0)3⋅X(k)
-
-
波形因子
-
T
F
13
=
∑
(
f
(
x
k
)
−
f
0
)
4
⋅
X
(
k
)
K
T_{F13} = frac{sum (f(x_k) - f_0)^4 cdot X(k)}{K}
TF13=K∑(f(xk)−f0)4⋅X(k)
-
3时间特征分析
- 干扰信号的频率(例如,每天发生的干扰次数)
- 干扰信号的持续时间
上述分别分析声发射信号和电磁~
问题二
已知在发生冲击地压危险前约7天内,电磁辐射和声发射信号存在随时间循环增大的趋势(如图2所示),这类信号我们称为前兆特征信号。在出现前兆特征信号之后的约7天内,有可能发生冲击地压,所以一般情况下出现前兆特征信号之后,会采取一定措施尽可能的防止冲击地压发生。应用附件1和2中的数据,完成以下问题。
第一问
取特征
(2.1) 建立数学模型,对电磁辐射和声发射信号中的前兆特征信号进行分析,重点分析信号的变化趋势,分别给出电磁辐射和声发射信号危险发生前(前兆特征)数据的**趋势特征(**不少于3个)。
第二问
建模,同问题一,这里自己换一个模型,别和问题一一样。
(2.2) 利用问题(2.1)中得到的特征,建立数学模型,对2020年4月8日-2020年6月8日及2021年11月20日-2021年12月20日的电磁辐射和2021年11月1日-2022年1月15日声发射信号中的前兆特征所在的时间区间进行识别,分别给出电磁辐射和声发射信号最早发生的5个前兆特征信号所在的时间区间,完成表3和表4。
| 表3 电磁辐射前兆特征时间区间 | ||
|---|---|---|
| 序号 | 时间区间起点 | 时间区间终点 |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
| 表4 声发射前兆特征时间区间 | ||
|---|---|---|
| 序号 | 时间区间起点 | 时间区间终点 |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
具体思路
第一问目标:分析电磁辐射和声发射信号中的前兆特征信号,提取相关的趋势特征。数据预处理 提取附件1中分类为’B’的数据(前兆特征信号)。 清理数据,确保时间和信号值格式正确,并处理可能存在的缺失值或异常值。趋势特征提取: 可以在问题一基础上新增一些熵指标,例如排列熵、模糊熵,近似熵等等。接着也是做识别,然后得不同时间段
统计和机器学习方法: 应用时间序列分析技术,如自回归模型(AR)、移动平均(MA)或ARIMA模型来分析信号趋势。 使用机器学习算法如随机森林或梯度提升机来识别前兆特征信号的模式。
第二问目标:根据第一问的分析结果,识别特定时间段内电磁辐射和声发射信号中的前兆特征时间区间。
问题三:实时前兆特征信号概率预测
为了尽早的识别前兆特征信号,在前兆特征信号出现的第一时间发出预警,需要在每次数据采集的时刻对危险进行预判。附件3给出了一些非连续时间段采集的电磁辐射和声发射信号数据。请建立数学模型,给出附件3中的每个时间段最后时刻出现前兆特征数据的概率,完成表5。
| 电磁辐射数据所在时刻 | 前兆特征的概率 | 声发射数据所在时刻 | 前兆特征的概率 |
| 2023-1-24 23:58:36 | 2023-1-24 23:58:36 | ||
| 2023-2-11 23:59:20 | 2023-2-11 23:59:20 | ||
| 2023-2-26 23:59:27 | 2023-2-26 23:59:27 | ||
| 2023-3-10 23:58:14 | 2023-3-10 23:58:14 | ||
| 2023-3-30 23:58:13 | 2023-3-30 23:58:13 |
思路
对于问题三,我们需要开发一个模型来在每次数据采集时刻预判冲击地压前兆特征信号的概率。
目标:建立数学模型,评估每个时间段最后时刻出现前兆特征数据的概率。
1数据整理: 从附件3中读取电磁辐射和声发射的数据。 检查数据完整性,处理缺失值或异常值。2特征工程: 提取每个时间段内的统计特征,例如均值、方差、最大值、最小值等。 根据问题一和问题二的结果,识别表明前兆特征的关键指标。
3模型建立3.1 时间序列分析: 分析各时间段数据的时间序列特性,识别周期性、趋势性变化。 使用时间序列预测模型(如ARIMA、指数平滑等)来预测短期内数据的走势。3.2 概率模型: 基于机器学习技术(如随机森林、梯度提升机),建立预测模型,输出为前兆特征的概率。
具体模型可以推荐:attention+lstm
附件
附件1 (Attachment 1).xlsx 附件2 (Attachment 2).xlsx 附件3 (Attachment 3).xlsx
GPT4打数模
如果不会写代码,可以问GPT。使用地址:我的GPT4
视频
B站会发:我的B站
以上就是关于2024五一杯:煤矿深部开采冲击地压危险预测 (详细完整思路,已修改)相关的全部内容,希望对你有帮助。欢迎持续关注程序员导航网,学习愉快哦!












