本文主要讲解关于轨迹规划 | 图解纯追踪算法Pure Pursuit(附ROS C++/Python/Matlab仿真)相关内容,让我们来一起学习下吧!
目录
- 0 专栏介绍
- 1 纯追踪算法原理推导
- 2 自适应纯追踪算法(APP)
- 3 规范化纯追踪算法(RPP)
- 4 仿真实现
-
- 4.1 ROS C++仿真
- 4.2 Python仿真
- 4.3 Matlab仿真
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 纯追踪算法原理推导
纯追踪算法(Pure Pursuit, PP)参考了人类驾驶行为,其基本思想是:在待跟踪路径上设置预瞄点(goal-ahead),通过简单的几何方法驱动机器人跟踪预瞄点,随着机器人运动,预瞄点动态移动直至抵达目标位置。
给定路径点
P
=
{
p
0
,
p
1
,
⋯
,
p
g
}
mathcal{P} =left{ boldsymbol{p}_0,boldsymbol{p}_1,cdots ,boldsymbol{p}_g right}
P={p0,p1,⋯,pg}。根据纯追踪算法设置的固定预瞄距离
L
L
L选择预瞄点
p
l
=
p
i
∈
P
s
.
t
.
∥
p
i
−
1
−
p
r
∥
2
2
<
L
a
n
d
∥
p
i
−
p
r
∥
2
2
⩾
L
boldsymbol{p}_l=boldsymbol{p}_iin mathcal{P} ,,mathrm{s}.mathrm{t}. left| boldsymbol{p}_{i-1}-boldsymbol{p}_r right| _{2}^{2}<L,,mathrm{and} left| boldsymbol{p}_i-boldsymbol{p}_r right| _{2}^{2}geqslant L
pl=pi∈Ps.t.∥pi−1−pr∥22<Land∥pi−pr∥22⩾L
其中
p
r
boldsymbol{p}_r
pr是最接近机器人当前位置的路径点。
当规划时间间隔
Δ
t
→
0
varDelta trightarrow 0
Δt→0时,可认为机器人线速度
v
v
v和角速度
ω
omega
ω不变,因此其转向半径
R
=
v
/
ω
R={{v}/{omega}}
R=v/ω是定值,即机器人进行圆周运动。
如图所示,根据几何关系可得
L
sin
2
α
=
R
sin
(
π
/
2
−
α
)
⇒
R
=
L
2
sin
α
frac{L}{sin 2alpha}=frac{R}{sin left( {{pi}/{2}}-alpha right)}Rightarrow R=frac{L}{2sin alpha}
sin2αL=sin(π/2−α)R⇒R=2sinαL
确定曲率半径后,对于差速轮式移动机器人而言,可根据下式计算当前的控制指令
{
v
t
=
v
d
ω
t
=
v
t
/
R
begin{cases} v_t=v_d\ omega _t={{v_t}/{R}}\end{cases}
{vt=vdωt=vt/R
在机器人局部坐标系中,设机器人与预瞄点的纵向误差为
e
y
e_y
ey,则
R
=
L
2
2
e
y
⇔
κ
=
2
L
2
⋅
e
y
R=frac{L^2}{2e_y}Leftrightarrow kappa =frac{2}{L^2}cdot e_y
R=2eyL2⇔κ=L22⋅ey
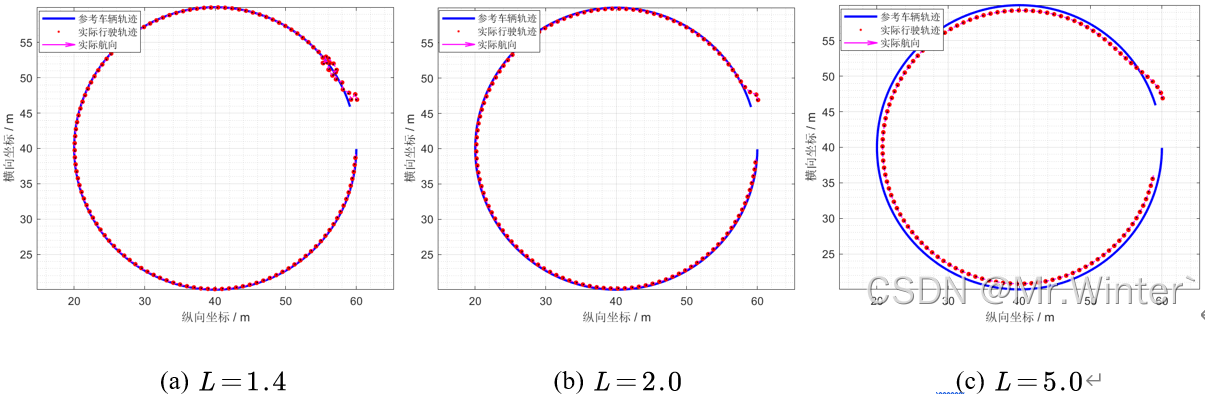
相当于一个以横向跟踪误差为系统误差的比例控制器,如图所示。增大
L
L
L有利于降低超调,但会产生稳态误差;减小
L
L
L能够加快动态响应速度,但容易引起振荡。
2 自适应纯追踪算法(APP)
为了在跟踪振荡和较慢收敛间取得可接受的权衡,自适应纯追踪算法(Adaptive Pure Pursuit, APP)根据运动速度自适应调整预瞄距离
L
t
=
l
t
v
t
+
L
0
L_t=l_tv_t+L_0
Lt=ltvt+L0
其中
l
t
l_t
lt是前瞻增益,表示将
v
t
v_t
vt向前投影的时间增量;
L
0
L_0
L0是最小预瞄距离。
3 规范化纯追踪算法(RPP)
考虑到机器人始终以期望速度 运动并不合理,尤其是在狭窄区域、急转弯等不完全可见工作空间,动态调整机器人速度有利于提供更高质量的行为表现。规范化纯追踪算法(Regulated Pure Pursuit, RPP)引入了修正启发式等进行自适应调整。举例而言,曲率启发式,目的是放慢机器人在部分可观察环境的速度,以提高盲转弯时的安全性。其中最大曲率阈值 提供了急转弯位置的速度缩放。
v
t
′
=
{
v
t
,
κ
⩽
κ
max
κ
max
κ
v
t
,
κ
>
κ
max
v_{t}^{'}=begin{cases} v_t,, , kappa leqslant kappa _{max}\ frac{kappa _{max}}{kappa}v_t,, , kappa >kappa _{max}\end{cases}
vt′={vt,κ⩽κmaxκκmaxvt,κ>κmax
可以根据应用需求设计更多启发式
4 仿真实现
4.1 ROS C++仿真
核心代码如下所示
bool RPPPlanner::computeVelocityCommands(geometry_msgs::Twist& cmd_vel)
{
...
double vt = std::hypot(base_odom.twist.twist.linear.x, base_odom.twist.twist.linear.y);
double L = getLookAheadDistance(vt);
getLookAheadPoint(L, robot_pose_map, prune_plan, lookahead_pt, theta, kappa);
double lookahead_k = 2 * sin(_dphi(lookahead_pt, robot_pose_map)) / L;
// calculate commands
if (shouldRotateToGoal(robot_pose_map, global_plan_.back()))
{
...
}
else
{
double e_theta = regularizeAngle(_dphi(lookahead_pt, robot_pose_map));
// large angle, turn first
if (shouldRotateToPath(std::fabs(e_theta), M_PI_2))
{
cmd_vel.linear.x = 0.0;
cmd_vel.angular.z = angularRegularization(base_odom, e_theta / d_t_);
}
// apply constraints
else
{
double curv_vel = _applyCurvatureConstraint(max_v_, lookahead_k);
double cost_vel = _applyObstacleConstraint(max_v_);
double v_d = std::min(curv_vel, cost_vel);
v_d = _applyApproachConstraint(v_d, robot_pose_map, prune_plan);
cmd_vel.linear.x = linearRegularization(base_odom, v_d);
cmd_vel.angular.z = angularRegularization(base_odom, v_d * lookahead_k);
}
}
return true;
}
4.2 Python仿真
核心代码如下所示
def plan(self):
lookahead_pts = []
dt = self.params["TIME_STEP"]
for _ in range(self.params["MAX_ITERATION"]):
# break until goal reached
if self.shouldRotateToGoal(self.robot.position, self.goal):
return True, self.robot.history_pose, lookahead_pts
# get the particular point on the path at the lookahead distance
lookahead_pt, _, _ = self.getLookaheadPoint()
# get the tracking curvature with goalahead point
lookahead_k = 2 * math.sin(
self.angle(self.robot.position, lookahead_pt) - self.robot.theta
) / self.lookahead_dist
# calculate velocity command
e_theta = self.regularizeAngle(self.robot.theta - self.goal[2]) / 10
if self.shouldRotateToGoal(self.robot.position, self.goal):
if not self.shouldRotateToPath(abs(e_theta)):
u = np.array([[0], [0]])
else:
u = np.array([[0], [self.angularRegularization(e_theta / dt)]])
else:
e_theta = self.regularizeAngle(
self.angle(self.robot.position, lookahead_pt) - self.robot.theta
) / 10
if self.shouldRotateToPath(abs(e_theta), np.pi / 4):
u = np.array([[0], [self.angularRegularization(e_theta / dt)]])
else:
# apply constraints
curv_vel = self.applyCurvatureConstraint(self.params["MAX_V"], lookahead_k)
cost_vel = self.applyObstacleConstraint(self.params["MAX_V"])
v_d = min(curv_vel, cost_vel)
u = np.array([[self.linearRegularization(v_d)], [self.angularRegularization(v_d * lookahead_k)]])
# update lookahead points
lookahead_pts.append(lookahead_pt)
# feed into robotic kinematic
self.robot.kinematic(u, dt)
return False, None, None
4.3 Matlab仿真
核心代码如下所示
while iter < param.max_iteration
iter = iter + 1;
% break until goal reached
if shouldRotateToGoal([robot.x, robot.y], goal, param)
flag = true;
break;
end
% get the particular point on the path at the lookahead distance
[lookahead_pt, ~, ~] = getLookaheadPoint(robot, path, param);
% get the tracking curvature with goalahead point
lookahead_k = 2 * sin( ...
atan2(lookahead_pt(2) - robot.y, lookahead_pt(1) - robot.x) - robot.theta ...
) / getLookaheadDistance(robot, param);
% calculate velocity command
e_theta = regularizeAngle(robot.theta - goal(3)) / 10;
if shouldRotateToGoal([robot.x, robot.y], goal, param)
if ~shouldRotateToPath(abs(e_theta), 0.0, param)
u = [0, 0];
else
u = [0, angularRegularization(robot, e_theta / param.dt, param)];
end
else
e_theta = regularizeAngle( ...
atan2(lookahead_pt(2) - robot.y, lookahead_pt(1) - robot.x) - robot.theta ...
) / 10;
if shouldRotateToPath(abs(e_theta), pi / 4, param)
u = [0, angularRegularization(robot, e_theta / param.dt, param)];
else
% apply constraints
curv_vel = applyCurvatureConstraint(param.max_v, lookahead_k, param);
cost_vel = applyObstacleConstraint(param.max_v, map, robot, param);
v_d = min(curv_vel, cost_vel);
u = [
linearRegularization(robot, v_d, param), ...
angularRegularization(robot, v_d * lookahead_k, param) ...
];
end
end
% input into robotic kinematic
robot = f(robot, u, param.dt);
pose = [pose; robot.x, robot.y, robot.theta];
end
完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇
以上就是关于轨迹规划 | 图解纯追踪算法Pure Pursuit(附ROS C++/Python/Matlab仿真)相关的全部内容,希望对你有帮助。欢迎持续关注程序员导航网,学习愉快哦!
转载请注明:轨迹规划 | 图解纯追踪算法Pure Pursuit(附ROS C++/Python/Matlab仿真) | 程序员导航网