本文主要讲解关于【研发日记】Matlab/Simulink技能解锁(七)——两种复数移相算法相关内容，让我们来一起学习下吧！

        复数移相，也称为复数相位旋转，就是在原有复数的基础上，不改变模数，只把相位角做一定的偏移。

文章目录

前言

三角函数移相

复数乘法移相

分析和应用

总结

前言

        见《【研发日记】Matlab/Simulink技能解锁(二)——在Function编辑窗口Debug》

        见《【研发日记】Matlab/Simulink技能解锁(三)——在Stateflow编辑窗口Debug》

        见《【研发日记】Matlab/Simulink技能解锁(四)——在Simulink Debugger窗口调试》

        见《【研发日记】Matlab/Simulink技能解锁(五)——七个Simulink布线技巧》

        见《【研发日记】Matlab/Simulink技能解锁(六)——六种Simulink模型架构》

三角函数移相

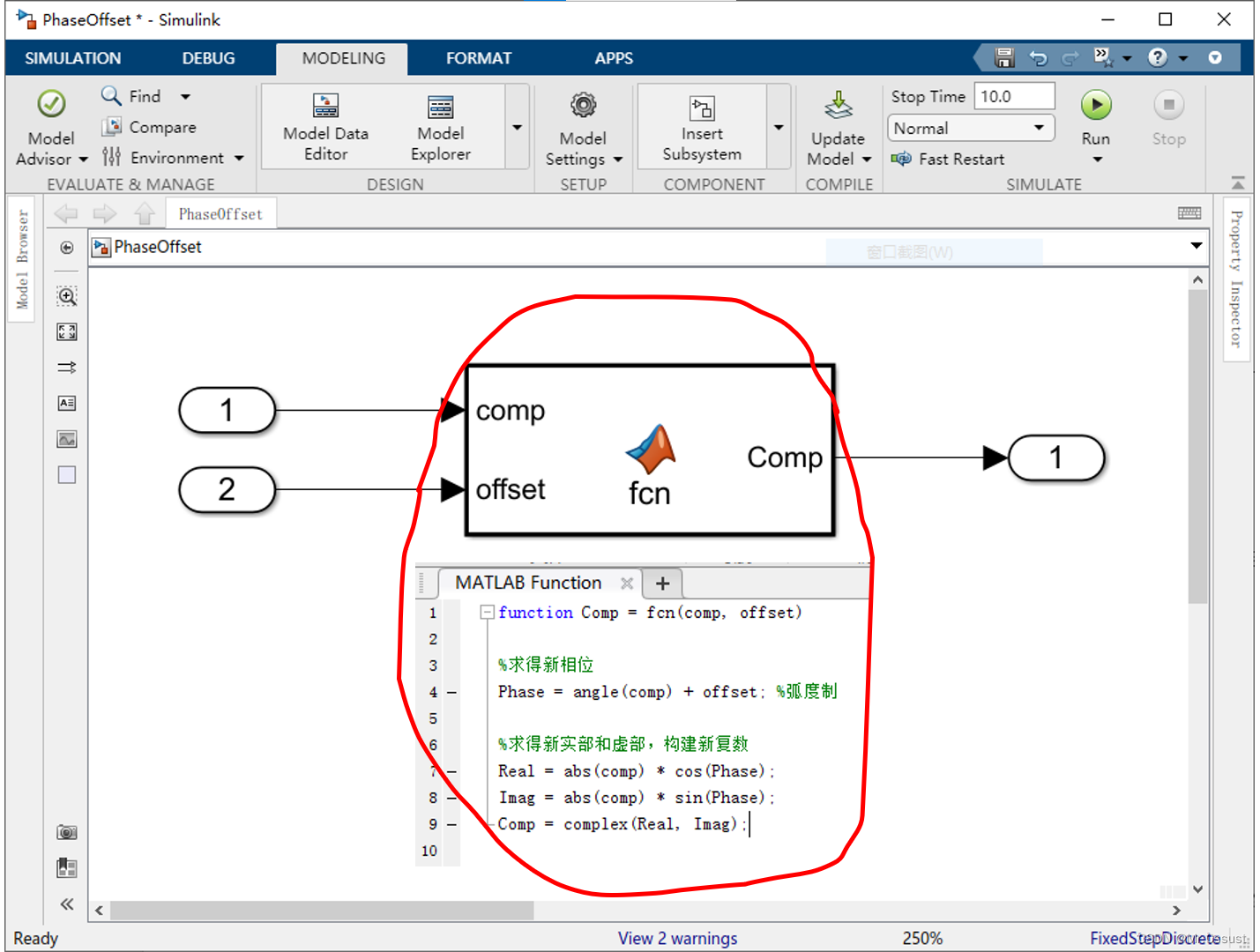
        三角函数移相法，是利用模数和实部虚部之间的三角函数关系，从原复数求得新复数。在Simulink中建立的移相函数，如下所示：

        Tips： offset的范围在-π到π之间，输入接口要做溢出处理。

        上述模型编译出来的代码，如下所示：

#include "PhaseOffset.h"
#include "PhaseOffset_private.h"

/* External inputs (root inport signals with default storage) */
ExtU_PhaseOffset_T PhaseOffset_U;

/* External outputs (root outports fed by signals with default storage) */
ExtY_PhaseOffset_T PhaseOffset_Y;

/* Real-time model */
static RT_MODEL_PhaseOffset_T PhaseOffset_M_;
RT_MODEL_PhaseOffset_T *const PhaseOffset_M = &PhaseOffset_M_;
real_T rt_atan2d_snf(real_T u0, real_T u1)
{
  real_T y;
  int32_T u0_0;
  int32_T u1_0;
  if (rtIsNaN(u0) || rtIsNaN(u1)) {
    y = (rtNaN);
  } else if (rtIsInf(u0) && rtIsInf(u1)) {
    if (u0 > 0.0) {
      u0_0 = 1;
    } else {
      u0_0 = -1;
    }

    if (u1 > 0.0) {
      u1_0 = 1;
    } else {
      u1_0 = -1;
    }

    y = atan2(u0_0, u1_0);
  } else if (u1 == 0.0) {
    if (u0 > 0.0) {
      y = RT_PI / 2.0;
    } else if (u0 < 0.0) {
      y = -(RT_PI / 2.0);
    } else {
      y = 0.0;
    }
  } else {
    y = atan2(u0, u1);
  }

  return y;
}

/* Model step function */
void PhaseOffset_step(void)
{
  real_T Out1_tmp;
  real_T Phase;

  /* MATLAB Function: '<Root>/MATLAB Function' incorporates:
   *  Inport: '<Root>/In1'
   *  Inport: '<Root>/In2'
   */
  Phase = rt_atan2d_snf(0.0, PhaseOffset_U.In1) + PhaseOffset_U.In2;
  Out1_tmp = fabs(PhaseOffset_U.In1);

  /* Outport: '<Root>/Out1' incorporates:
   *  MATLAB Function: '<Root>/MATLAB Function'
   */
  PhaseOffset_Y.Out1.re = Out1_tmp * cos(Phase);
  PhaseOffset_Y.Out1.im = Out1_tmp * sin(Phase);
}

/* Model initialize function */
void PhaseOffset_initialize(void)
{
  /* Registration code */

  /* initialize non-finites */
  rt_InitInfAndNaN(sizeof(real_T));
}

/* Model terminate function */
void PhaseOffset_terminate(void)
{
  /* (no terminate code required) */
}

复数乘法移相

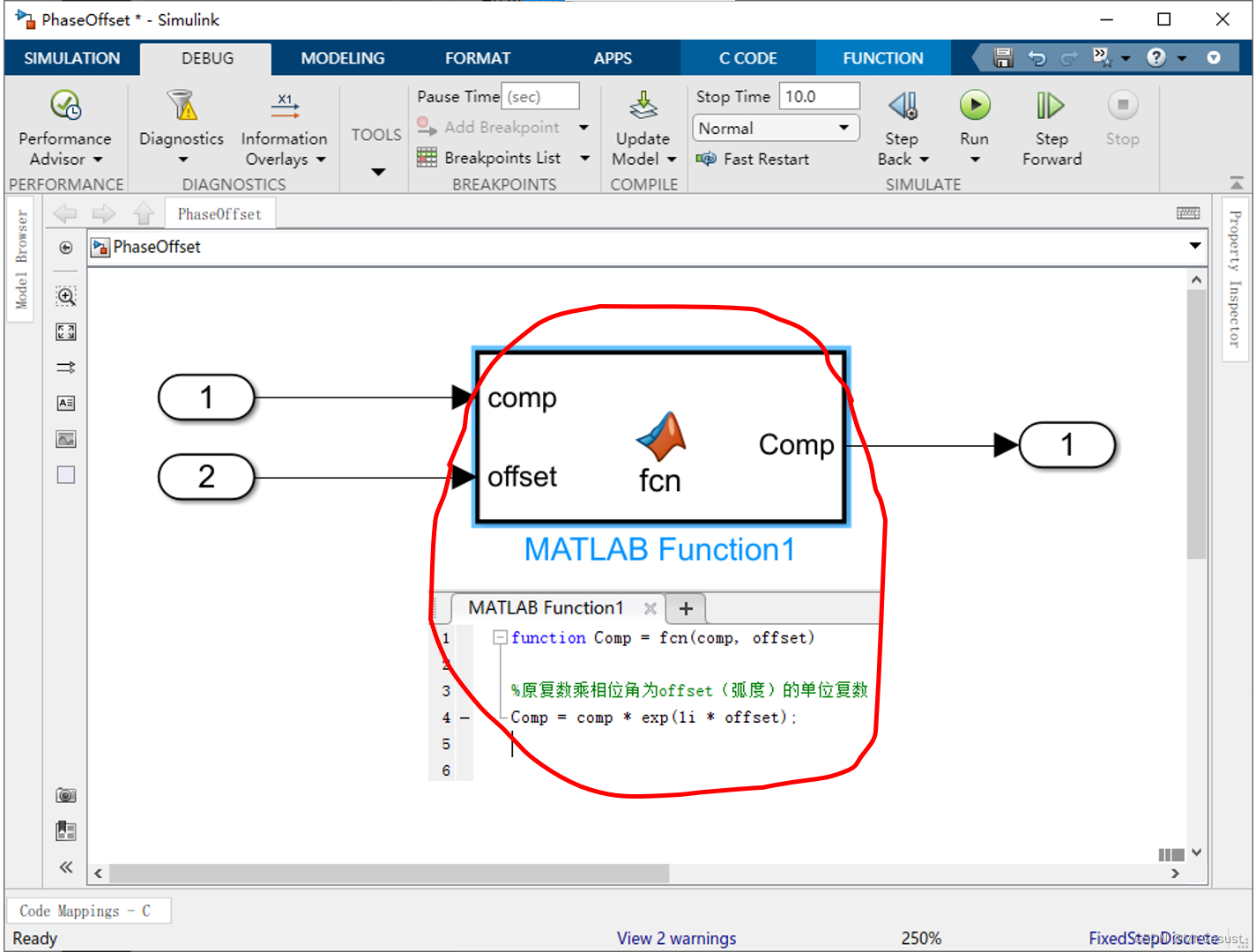
        当一个复数乘以另一个相位角为θ的复数时，那么前者的相位就会偏移θ。如果后者是单位复数（模数为1），那么前者的模数不变，只跟随θ旋转相位角。用这种算法建立的移相函数如下所示：

        Tips：exp(1i * offset) = cos(offset) + sin(offset)i。

        上述模型编译出来的代码，如下所示：

#include "PhaseOffset.h"
#include "PhaseOffset_private.h"

/* External inputs (root inport signals with default storage) */
ExtU_PhaseOffset_T PhaseOffset_U;

/* External outputs (root outports fed by signals with default storage) */
ExtY_PhaseOffset_T PhaseOffset_Y;

/* Real-time model */
static RT_MODEL_PhaseOffset_T PhaseOffset_M_;
RT_MODEL_PhaseOffset_T *const PhaseOffset_M = &PhaseOffset_M_;

/* Model step function */
void PhaseOffset_step(void)
{
  real_T r;
  real_T y_re;

  /* MATLAB Function: '<Root>/MATLAB Function1' incorporates:
   *  Inport: '<Root>/In2'
   */
  if (PhaseOffset_U.In2 == 0.0) {
    y_re = exp(PhaseOffset_U.In2 * 0.0);
    r = 0.0;
  } else {
    r = exp(PhaseOffset_U.In2 * 0.0 / 2.0);
    y_re = r * cos(PhaseOffset_U.In2) * r;
    r *= r * sin(PhaseOffset_U.In2);
  }

  /* Outport: '<Root>/Out1' incorporates:
   *  Inport: '<Root>/In1'
   *  MATLAB Function: '<Root>/MATLAB Function1'
   */
  PhaseOffset_Y.Out1.re = PhaseOffset_U.In1 * y_re;
  PhaseOffset_Y.Out1.im = PhaseOffset_U.In1 * r;
}

/* Model initialize function */
void PhaseOffset_initialize(void)
{
  /* (no initialization code required) */
}

/* Model terminate function */
void PhaseOffset_terminate(void)
{
  /* (no terminate code required) */
}

分析和应用

        复数移相在嵌入式软件开发中应用非常广泛，尤其是在电源设计和电机控制领域。上述两种移相算法都能实现相同的功能，但是具体运算过程略有差别，可以从两者的C代码中进行分辨。

        三角函数移相主要用到的运算是arctan()、abs()、cos()、sin()等，复数乘法移相主要用到的运算是e^()、cos()、sin()等，其中的abs()实质是平方和开方，e^()也是n次方，所以底层运算基本上都是一样的。

        在matlab函数中，复数乘法移相的运算步骤更加精简。在底层C代码中，三角函数移相的运算步骤更加精简。

        综上，可以根据自己的开发理念选取合适的移相算法。如果注重运行高效，就选择三角函数移相。如果注重开发代码精炼的，就选择复数乘法移相。

总结

        以上就是本人在研发中使用Simulink开发复数移相算法时，一些个人理解和分析的总结，主要介绍了两种移相算法的工作原理，展示了算法运行的效果，并分析了这两种算法的特点和适用场景。

        后续还会分享另外几个最近解锁的Matlab/Simulink新技能，欢迎评论区留言、点赞、收藏和关注，这些鼓励和支持都将成文本人持续分享的动力。

        另外，上述例程使用的Demo工程，可以到笔者的主页查找和下载。

        版权声明，原创文章，转载和引用请注明出处和链接，侵权必究！

以上就是关于【研发日记】Matlab/Simulink技能解锁(七)——两种复数移相算法相关的全部内容，希望对你有帮助。欢迎持续关注程序员导航网，学习愉快哦！